はてなアプリケーションエンジニアの ![]() id:takuya-a です。
id:takuya-a です。
この記事では、Microsoft の検索エンジン Bing で採用された BitFunnel アルゴリズムを紹介します。 昨年のエンジニアアドベントカレンダーでは、文字列検索のアルゴリズム全般について紹介しました(文字列アルゴリズムの学びかた - Hatena Developer Blog)。今年はそのなかでも、インデックス(索引)を使った全文検索アルゴリズムについてのお話になります。
この記事の前半は全文検索の入門にもなっていますので、検索技術になじみがない方にも楽しんでいただけるのではないでしょうか。 逆に、「そんなのもう知ってるよ!」という方は、本題である「BitFunnel アルゴリズムの詳細」から目を通していただければと思います。
この記事は、はてなエンジニア Advent Calendar 2017の21日目の記事です。昨日は ![]() id:kizkoh さんによる Redis Cluster の運用とモニタリング/監視のコツでした。明日は
id:kizkoh さんによる Redis Cluster の運用とモニタリング/監視のコツでした。明日は ![]() id:pokutuna さんです!
id:pokutuna さんです!
- BitFunnel アルゴリズムの概要
- 全文検索アルゴリズム概説
- 転置インデックス方式の全文検索
- シグネチャファイル方式の全文検索
- BitFunnel アルゴリズムの詳細
- Higher Rank Rows (1) - 基本
- Higher Rank Rows (2) - Rank 1 Row の構築
- Higher Rank Rows (3) - Higher Rank Rows の誤検知率
- Higher Rank Rows (4) - Rank 1 Row での検索
- Higher Rank Rows (5) - Rank 1 以上の Higher Rank Rows
- Frequency Conscious Signatures
- Sharding by Document Length
- BitFunnel アルゴリズムのパフォーマンス
- BitFunnel アルゴリズムを全文検索に使うときの注意点
- まとめ
- 参考文献
- さらに学ぶために
BitFunnel アルゴリズムの概要
ひとことで言うと
- これまで技術的な課題があって使われてこなかったシグネチャファイルという古典的な手法を、数々のテクニックで改善し、プロダクションまでもっていった、めちゃくちゃかっこいいアルゴリズム
シグネチャファイルの復権
現在の主要な Web 検索エンジンは、転置インデックス (inverted index) と呼ばれる方式が一般的です。 BitFunnel アルゴリズムでは、シグネチャファイル (signature file) (または単に シグネチャ (signature))という古典的な方式をベースに、いくつもの独自アルゴリズムを開発・統合しています。
Microsoft が公開している BitFunnel の解説動画によると、Bing の検索サーバを BitFunnel アルゴリズムベースに切り替えたところ、検索クエリのレイテンシが約1/2になった と紹介されています(緑、赤、青は各 BitFunnel インスタンスのレイテンシ時系列)。
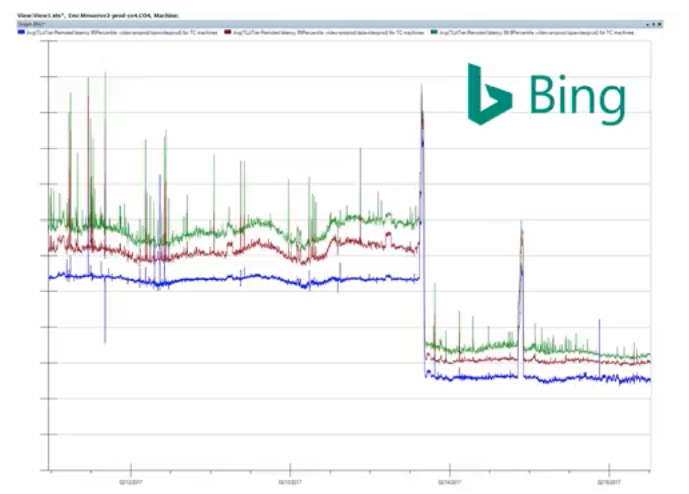
BitFunnel アルゴリズムの詳細は、Microsoft が SIGIR 2017 *1で発表した論文「BitFunnel: Revisiting Signatures for Search」に書かれています*2。
記事の後半で、転置インデックス方式や従来のシグネチャファイル方式とも対比しながら、BitFunnel アルゴリズムの詳細について、できるだけわかりやすく解説していきます。
BitFunnel という用語について
BitFunnel という単語は、文脈によっていくつかの意味で使われているので、なにを指しているか注意が必要です。
- 論文で発表されているアルゴリズムの名前
- Bing のバックエンドで使われている検索エンジンシステムの名前
- オープンソース化されている検索エンジンライブラリ・システムの名前
この記事では、主に 1 のアルゴリズムを表す場合は「BitFunnel アルゴリズム」、2 のシステムを表す場合は単に「BitFunnel」と表記することにします(3 については今回は扱いません)*3。
BitFunnel についての参考リンク
- BitFunnel: Revisiting Signatures for Search - YouTube
- Microsoft による解説動画
- この記事の画像はほとんどこの動画から引用しています
- BitFunnel: Revisiting Signatures for Search
- 記事執筆の参考にした論文
- 全文 PDF へのリンクあり
- 自分のブログに論文を読んだメモを置きました
- BitFunnel
- BitFunnel アルゴリズムをベースにオープンソース化された検索ライブラリ BitFunnel のリポジトリなどが公開されている
- bitfunnel.org
- BitFunnel の公式サイト
- デザインノートや開発者によるブログなど
- 米Microsoft、オープンソースの全文検索システム「BitFunnel」を公開 | OSDN Magazine
- BitFunnel が OSS 化されたときの記事
全文検索アルゴリズム概説
BitFunnel アルゴリズムの詳細に入る前に、全文検索について軽く振り返ってみましょう。
全文検索の目的は、検索対象となる複数の 文書集合 (document collection) のなかから、文字列からなる 検索質問 (query; クエリ) にマッチする 文書 (document) を探し出すことです。
全文検索のアルゴリズムは、大まかに以下の2つにわけられます(参考: 文字列アルゴリズムの学びかた - Hatena Developer Blog)。
- 逐次型(インデックスを使わない全文検索アルゴリズム)
- KMP, BM など
- grep などの文字列検索プログラムで実装されている
- インデックス型(インデックスを使う全文検索アルゴリズム)
- 転置インデックス、シグネチャファイル、接尾辞配列 (SA)、FM-index など
- 何らかのデータ構造からなるインデックス(索引)を構築、ファイルなどに保存し、検索のときに利用する
逐次型の全文検索アルゴリズムはインデックスを構築しなくてもよいため、手軽に使える反面、検索対象の文書数が多いと、レスポンスが非常に遅くなってしまうという問題があります。
一方のインデックス型は、工夫次第で超大規模な検索対象にも対応できます。その代わり、インデックスの構築や管理にコストがかかります。
検索エンジンと全文検索アルゴリズム
全文検索アルゴリズムのもっとも有名な応用は、Google 検索に代表される Web 検索エンジンでしょう。 Web 検索では大量の Web ページを検索対象とするため、ほぼ例外なくインデックス型の全文検索アルゴリズムが使われます。
Web ページをインデックスする Web 検索エンジン以外にも、いろいろな検索エンジンがあります。 たとえば Windows OS に搭載されている Windows Search は、PC に入っているファイルをインデックスして検索することができます。 MacOS にも同様の Spotlight という検索エンジンが同梱されています。
ここでは、そういった検索エンジンを例として、代表的な全文検索アルゴリズムを簡単に解説します。
検索エンジンでのインデックスの構築と検索
検索エンジンのコア(クロールなどは含めない)の役目は、大きく分けると2つしかありません。 1つは インデックスの構築 、もう1つは クエリ文字列による検索 です。 簡単にまとめると、それぞれ以下のことをやっているだけです。
- インデックスの構築
- それぞれの文書にIDを付与
- 文書をトークン(単語など)*4の列に分割
- トークン列をもとにインデックスを構築・更新
- クエリ文字列による検索
- クエリをトークン(単語など)の列に分割
- インデックスを使ってヒットする文書IDのリストを取得する
- 文書IDのリストにスコアをつけてソートした結果を返す
このなかで、インデックス構築では 3. トークン列をもとにインデックスを構築・更新 の部分、検索では 2. インデックスを使ってヒットする文書IDのリストを取得する の部分が、全文検索アルゴリズムの関わる処理になります。
インデックス型の全文検索アルゴリズムには、上述の通り多数の方式がありますが、なかでも「転置インデックス方式」と「シグネチャファイル方式」の2つを紹介します。
転置インデックス方式の全文検索
転置インデックス法 (inverted index method) は、非常にポピュラーな全文検索の方式です。 転置インデックスとよばれるデータ構造を構築し、それを使って非常に高速に文書IDのリストを取得します。
転置インデックス方式では、単語ベースのインデックスを作る方法と、文字ベースのインデックスを作る方法の2つがあります。 単語ベースのインデックスでは、テキストの文字列を トークナイザ (tokenizer) (日本語の場合は形態素解析器を使用することが多い)によってターム(単語)に分割し、それをもとにインデックスを構築します。 一方、文字ベースのインデックスでは、基本的には N-gram という方式でテキストの部分文字列を生成し、それをもとにインデックスを構築します。
ここでは単語ベースのインデックスを前提に、転置インデックスを説明します。
転置インデックス方式の特徴
- ターム(単語)に紐づく文書IDリストだけを走査すればよいため、検索が高速です。
- 逐次検索が必要ないため、比較的スケーラビリティが高い手法です。
- AND/OR を駆使した複雑なクエリに対しても、それらのクエリ処理アルゴリズムがよく研究されており、安定したパフォーマンスを発揮します*5。
- 単語ベースのインデックスでは、誤検出 (false positive) が基本的にはありません(それらを許容する pruning というテクニックもありますが、実装されている例は多くありません)*6。
- 一方で、単語ベースのインデックスでは、トークナイズ処理の失敗(形態素解析のミスなど)で文書の取りこぼし (false negative) が起こる可能性があります*7。
- インデックスサイズは後述するシグネチャファイルと比べると大きくなりますが、転置インデックスのポスティングリスト(文書IDのリストの部分)は差分圧縮(差分符号化による圧縮アルゴリズム)と相性がよく、インデックスの表現をコンパクトにすることができます。
転置インデックスの抽象データ構造
転置インデックスは、概念的には、 ターム(単語) -> 文書IDのリスト という、いわゆるマップやハッシュテーブルのようなデータ構造です。
ターム(単語)をキーにして、そのタームを含む文書IDのリストが取り出せるようになっています。
実際には、文書IDのほかにもターム(単語)の出現位置 (position) もしくは出現頻度 (term frequency) も保存するのですが、今回は簡単のために省略します*8。
文書IDのリストは、圧縮率や検索アルゴリズムの速度のために、文書IDで昇順にソートすることが多いです。
転置インデックスがどういうデータ構造なのか、具体例をみていきましょう*9。
転置インデックスの構築
たとえば以下のような2つの文書があったとします。それぞれの文書IDを 1、 2 とします。
[文書1] big brown dog [文書2] small crazy dog
文書1、文書2の本文
文書を順番に読んで、転置インデックスを構築していきます。
1つめの文書は big / brown / dog という3つのターム(単語)に分けることができます。
転置インデックスは 単語 -> 文書IDのリスト という構造でした。
文書1の文書IDは 1 なので、文書IDのリストは 1 という値だけをもつリスト [1] になります。
よって、1つめの文書で構築した転置インデックスはこうなります。
big [1] brown [1] dog [1]
文書1から構築した転置インデックス
2つめの文書は small / crazy / dog という3つのターム(単語)に分けることができます。
これをもとに、先ほど構築した転置インデックスに追記します。
新しく出てきた単語 (small crazy) については、転置インデックスに新しくキーを追加します。
すでにある単語 (dog) については、転置インデックスにキーでアクセスして、文書IDのリスト [1] を取り出し、後ろに文書2の文書ID 2 を追記します。
最終的な転置インデックスは以下のようになります。
big [1] brown [1] crazy [2] dog [1, 2] small [2]
文書1、文書2から構築した転置インデックス
単語分割さえできれば簡単に構築できることがわかりますね。
ただし、実際の転置インデックス構築では、メモリ効率や速度のために、ここで紹介したのとは異なる方法でやっていることが多いです。 また、転置インデックスの物理的なデータ構造では、単語の文字列ではなく、単語IDを使います。 単語文字列と単語IDのマッピングを保存する辞書を別に構築します。 文書IDのリストも、差分符号化したものを圧縮して保存します。
転置インデックスを使った検索
big という単語で検索することを考えてみます。
先ほど構築した転置インデックスを見てみましょう。
big [1] brown [1] crazy [2] dog [1, 2] small [2]
文書1、文書2から構築した転置インデックス(再掲)
転置インデックスで big というキーで文書IDのリストを取り出すと、文書ID 1 のみが入っていることがわかります。
この文書IDを返せば検索は完了です*10。
また、 dog というキーで文書IDのリストを取り出すと、文書ID 1 と 2 の両方がヒットします。
シグネチャファイル方式の全文検索
シグネチャファイル法 (signature file method) (シグネチャ法 (signature method) 、特徴ベクトル法 (signature vector method) とも)は、転置インデックスと同様、インデックスを使う全文検索の方式です(Wikipedia)。
情報検索の分野で古くからある手法で、シグネチャ(直訳すると署名)というデータ構造をインデックスとして使用します。 文書ごとにシグネチャを作成し、そのシグネチャをチェックすることで検索を行います。
文書ごとに作成するシグネチャを 文書シグネチャ (document signature) と呼びます。 知っている方向けに説明すると、この文書シグネチャというのは要するにブルームフィルタのことです*11。
文書シグネチャは、文書に含まれるすべての単語の 単語シグネチャ (word signature) を「重ね書き」したものです。 単語シグネチャ、文書シグネチャの作り方は、このあとの「シグネチャファイルの構築」でくわしく見ていきます。
ここで言っているシグネチャというのは、実体としてはただのビットベクトルです*12。 シグネチャファイルでの検索は、これらのビットベクトルに対してビット演算を繰り返すことに他なりません。
シグネチャファイル方式の特徴
シグネチャファイル方式では、他の手法と比較して、インデックスサイズは非常に小さくなります(ビットベクトルのサイズにもよりますが)。 一方で、いくつかの実用上の問題があり、全文検索の用途では現在あまり使われていません。
とくに問題なのが、確率的に 誤検出 (false positive) (フォルスドロップと呼ばれる)が発生することです。 誤検出の確率を小さくするためには、ビットベクトルのサイズを大きくすればよいのですが、インデックスサイズが大きくなりますし、誤検出を0にすることはできません。
通常の実装では、ヒットした文書に対してフォルスドロップのチェックを行うために、逐次型の全文検索を行う必要がでてきます。 もちろん、転置インデックスと比較すると、パフォーマンスは非常に悪くなります。 そのため、 小規模なコレクション(文書集合)にしか有効ではないと考えられていました。
それでは、シグネチャファイルの作り方をみていきましょう。
シグネチャの構築 (1)
まずは、先ほど登場した文書1のみを使って説明していきます。本文は以下の通りです(この文書は、解説動画で出てくる例そのものです)。
[文書1] big brown dog
文書1の本文
文書は big / brown / dog という3つの単語(ターム)からなります。
この文書のシグネチャ(文書シグネチャ)を計算してみましょう。
ただし、以下の説明では、わかりやすさのためにアルゴリズムの効率は度外視しています。 また、長々と書いていますが、英語が苦でなければ解説動画のほうが手っ取り早いと思います(ちなみに、自動翻訳の日本語字幕も見られますが意味不明です)。
シグネチャの構築 (2) - 単語シグネチャの計算
文書シグネチャとして、今回は16ビットのビットベクトルを用意します*13。
0000 0000 0000 0000
文書1の文書シグネチャ(初期状態)
単語(ターム)を入力とし、ビット位置のリストを出力する関数 H(t) を構成します(t はターム文字列)。
H(t) は k 個のハッシュ関数を使って計算されます。
今回は k = 3 として、それぞれのハッシュ関数を h1(t) h2(t) h3(t) としましょう。
それぞれのハッシュ関数は、0から15までの16種類の数字(これは文書シグネチャにおけるビット位置を表します)のうち、1つを出力するような関数を選びます*14。
各ハッシュ関数の計算結果はたとえば以下のようになります。
h1('big') = 3
h2('big') = 14
h3('big') = 7
単語 big のハッシュ値
H(t) は、それぞれのハッシュ値(つまりビット位置)を重複排除(uniq)したリストを出力します。
つまり、H(t) が返す値は、高々 k 個 です。
H('big') = [3, 7, 14]
単語 big に対する H(t) の出力
16ビットのビットベクトルに対して、H('big') が出力したビット位置に 1 を立てていきます。
こうして単語ごとにつくったシグネチャを単語シグネチャと呼びます。
もちろん、単語シグネチャで立っているビットも高々 k 個になります。
0001 0001 0000 0010
単語 big の単語シグネチャ
シグネチャの構築 (3) - 文書シグネチャの計算
単語ごとに単語シグネチャを計算し、文書シグネチャに重ね書きしていきます。
次の単語 brown の単語シグネチャを計算します。
0100 0100 0100 0000
単語 brown の単語シグネチャ
ここまでの文書シグネチャは以下のようになります。
big 0001 0001 0000 0010
brown 0100 0100 0100 0000
--------------------------
0101 0101 0100 0010
単語 big brown の単語シグネチャを書き込んだ文書シグネチャ(作りかけ)
dog の単語シグネチャも同様に計算します。
0001 0000 0001 0001
単語 dog の単語シグネチャ
同様に、さきほどの文書シグネチャに書き込んだら完成です。
dog 0001 0000 0001 0001
0101 0101 0100 0010 <- 先ほどの文書シグネチャ(作りかけ)
-------------------------
0101 0101 0101 0011 <- 完成した文書シグネチャ
文書1の文書シグネチャ(完成形)
シグネチャを使った検索 (1) - 文書に含まれないタームで検索
それでは、文書シグネチャを使って、文書1 big brown dog に対して検索をしてみましょう。
文書1には含まれていない、cat という単語でシグネチャファイル方式での検索を実行してみます。
まず、検索語 cat の単語シグネチャを計算します。
1000 0100 0000 0001
単語 cat の単語シグネチャ
文書1の文書シグネチャとビット単位で比較します。
cat 1000 0100 0000 0001 <- 単語シグネチャ
0101 0101 0101 0011 <- 文書シグネチャ
0番目の位置のビットが文書シグネチャに含まれていないことがわかります。
cat という単語が文書シグネチャに書き込まれていれば、cat の単語シグネチャのすべての 1 が含まれているはずですよね。
つまり、文書1には cat が 含まれていないことが確実にわかります(これが、シグネチャファイル方式には誤検出 (false positive) はあっても取りこぼし (false negative) がないことの理由です)。
以上で見たように、シグネチャを使った検索では、 単語シグネチャ & 文書シグネチャ == 単語シグネチャ という条件をチェックしていることになります(& は論理積のビット演算子)。
シグネチャを使った検索 (2) - 文書に含まれるタームで検索
次に、文書1 big brown dog に含まれている big という単語で検索してみます。
big の単語シグネチャは以下の通りでした。
0001 0001 0000 0010
単語 big の単語シグネチャ
先ほどと同じように、文書1の文書シグネチャとビット単位で比較します。
big 0001 0001 0000 0010 <- 単語シグネチャ
0101 0101 0101 0011 <- 文書シグネチャ
big の単語シグネチャのすべての 1 が、文書シグネチャに含まれています。
実は、これでわかるのは、単語 big が文書1に 含まれていそう ということだけです。
なぜなら、シグネチャファイルでは誤検出 (false positive) が発生するからです。
次の例をみてみましょう。
シグネチャを使った検索 (3) - 誤検出
こんどは、文書1 big brown dog に含まれていない house という単語で検索してみましょう。
house の単語シグネチャが以下のようになったとします。
0100 0100 0001 0000
単語 house の単語シグネチャ
これは、 big brown dog の単語シグネチャのどれとも異なっています。
文書シグネチャと比較してみます。
house 0100 0100 0001 0000 <- 単語シグネチャ
0101 0101 0101 0011 <- 文書シグネチャ
単語シグネチャのすべての 1 が、文書シグネチャに含まれています!
big brown dog の単語シグネチャのどれとも異なっていたのに、です。
つまり、シグネチャファイル方式では、文書に含まれていない単語でもヒットする可能性があります。 シグネチャはハッシュ関数を通して計算されたものですから、こういった誤検出 (false positive) は、ある意味、確率的に発生するということになります。
シグネチャを使った検索 (4) - 複数の文書から検索
複数の文書から検索するときには、すべての文書の文書シグネチャを、単語シグネチャとの論理積 (AND) をとってチェックしていけばいいことがわかります。
この例では、A - P の16文書に対して、単語シグネチャ 0010 0100 0100 0000 で検索しています。
すべての文書シグネチャとのビット演算を行って、最終的に3つの文書 (B, F, L) がマッチすることがわかりました。
なお、複数の文書シグネチャを1つのファイルにまとめたものを シグネチャファイル (signature file) と呼びます。
Bit-String シグネチャ
これまで見てきたようなシグネチャの方式を Bit-String シグネチャ (bit-string signature) といいます。
この方式は、すべての文書シグネチャのビットを読み込む必要があるので、実は効率があまりよくありません。
例えば、文書シグネチャが1,600ビット、文書数が100万あったとすると、 200bytes * 1M = 200MB の read が必要です。
Web 検索では文書数はさらに多く、たとえば低く見積もって1億としても、文書シグネチャの全体は 20GB になります。
検索のたびに 20GB ものデータを読むのは現実的ではありません。
次の節では、もっと効率的なシグネチャの方式である、Bit-Sliced シグネチャをみていきます。
Bit-Sliced シグネチャ
Bit-String シグネチャは検索のためにすべての文書シグネチャを読み込む必要があります。 これから紹介する Bit-Sliced シグネチャ (bit-sliced signature) を使うと、検索精度を犠牲にすることなく検索時に読み込むビット数を劇的に減らすことができ、結果として高速に結果を返せます。
端的にいうと、Bit-Sliced シグネチャは Bit-String シグネチャを「転置」したものです。

単語シグネチャ(Query の部分)の 1 の部分だけをチェックすればいいのですから、ビット位置 2 5 9 の行だけを読み込めばそれで事足ります。
シグネチャを1,500ビット、 k = 6 とすると、転置するだけで読み込むビット数が 6/1500 (= 0.4%)と激減しています。
イメージ的には、転置インデックスで、単語に紐づいている文書IDのリストを走査しているのに近いですね(転置インデックスは、こうやって必要なデータだけを読むことで高速な検索を実現しているのでした)。
Bit-Sliced シグネチャで検索を実行するには、この3行がすべて 1 になっている列(文書)を探せばOKです。

Bit-Sliced シグネチャでの検索は、読み込むビット数 (I/O) が減っただけでなく、CPU レベルでも高速に実行できるようになっています。
どういうことかというと、 k の値、つまりチェックする行数は(Web 検索の規模ですら)10にも満たないので、1回のALU演算で実行できてしまうのです!
さて、チェックする行数は k だけになり、劇的に速くなったシグネチャ方式の検索ですが、実はまだ速くする余地があります。
Bit-Sliced シグネチャの検索で読み込まないといけない列は、文書数だけあり、それは Web 検索においては億のオーダーです。 転置インデックスでは、検索語を実際に含んでいる文書IDだけを読み込んでいました。 単語の文書頻度(その単語を含む文書の数。DF)にもよりますが、おおよその単語でこれは全文書数より何桁も少ない数です。
この問題を解決するのが BitFunnel アルゴリズムの一角である Higher Rank Rows です。
BitFunnel アルゴリズムの詳細
BitFunnel アルゴリズムは、シグネチャファイル方式を踏襲しつつ、その問題点を解決するテクニックを組み込んだ全文検索アルゴリズムです。
BitFunnel アルゴリズムで使われた技術は以下の3つです。
- Higher Rank Rows
- Frequency Conscious Signatures
- Sharding by Document Length
以下の解説動画に沿って、ひとつずつ紹介してきます。
Higher Rank Rows (1) - 基本
Bit-Sliced シグネチャでは、1つの行に対して、文書の数だけビットを読み込まないといけないのが問題でした(k 行を読み込むので、 N を文書数とすると合計で kN ビット)。
これを減らす方法を考えます。
たとえば、読み込むビットを半分にすることはできるでしょうか?
Higher Rank Rows では、文書の数だけあったビットを「折りたたむ」ことで、これを実現しています(以下の説明は、6:30 あたりからの解説動画のアニメーションを見ながら読むと、より理解しやすいと思います)。
Higher Rank Rows (2) - Rank 1 Row の構築
Bit-Sliced シグネチャの方法でつくった、もとの行(Rank 0)を、以下のように半分に分割します。
Rank 0 0110 0100 0101 0110
--------- ---------
(1) (2)
2つのビット列の論理和 (OR) をとります。
(1) 0110 0100 (2) 0101 0110 ---------------- (1|2) 0111 0110
これが、もとの行より1つ高い、Rank 1 の行です。
Higher Rank Rows (3) - Higher Rank Rows の誤検知率
Rank 1 の行の1つのビットには、Rank 0 の2つのビットが対応していることになります。
検索するときには、Rank 0 の行を「復元」してマッチさせてみればよいわけです。
実際に「復元」してみた行が以下です。
Rank 0' 0111 0110 0111 0110
--------- ---------
(1|2) (1|2)
ここで、Rank 0 と Rank 0' を比べてみると、すこし 1 が増えているのがわかりますね。
それは、先ほど論理和 (OR) をとったからです。
もちろん、Rank 1 での 1 が、 Rank 0 で 1 だったか、それとも 0 だったのかは、もはやわからなくなります。
つまり、表現がコンパクトになった代償として、検索時には誤検知 (false positive) が発生しやすくなります。
Higher Rank Rows (4) - Rank 1 Row での検索
先ほどから「復元」という表現を使っていますが、実際には、本当にメモリ上にビット列を復元する必要はなく、ビット列のオフセットをずらして読むだけでできます。 つまり、読み込む必要のあるビット数は、半分で済みます。
Bit-Sliced シグネチャでは、複数の行(最大で k 行)を読んで、論理積 (AND) をとるのでした。
こうやってもとの行を「復元」しながら検索を実行するので、ある行では Rank 0 を使い、別の行では Rank 1 を使って検索する、ということもできます。
Row 1 0111 0110 Row 0 0010 0001 0100 0010 ---------------------------- Row 1' 0111 0110 0111 0110 Row 0 0010 0001 0100 0010 ---------------------------- Match 0010 0000 0100 0010
Row 1 は Rank 1 の行、 Row 1' は Row 1 から Rank 0 を「復元」した行です。
Row 1' と Row 0 の論理積 (AND) を取ると、3つの文書がヒットしました。
Higher Rank Rows (5) - Rank 1 以上の Higher Rank Rows
Rank 1 をつくった方法を繰り返していけば、Rank 2, Rank 3 ... と、1ビットになるまで続けることができます。

図では、 Rank 5 で 1 だけになっていますが、これを使って Rank 0 を復元すると、すべて 1 のビット列になります。
1ビットだけ読めば検索は実行可能なので、当然クエリ処理は速くなりますが、いかにも誤検知が発生しそうですね。 実は、誤検知を確実に一定以下に抑えるという条件のなかで、最も高いランクを選ぶ、という最適化をすることができます(ランクというパラメータを最大化する、制約つきの最適化です)。
ただし、単語ごとに行のビット密度が異なるため、誤検知の起こりやすさも変わってきます。 よって、単語ごとに(= 逆文書頻度 (IDF; Inversed Document Frequency) ごとに)最適なランクは異なるので、それぞれ別々に最適化することになります。
この最適化については、論文の5章 "Performance Model and Optimization" に理論的な導出も含めて詳しく書かれています。 BitFunnel アルゴリズムでは、次の節で説明する Frequency Conscious Signatures のパラメータと合わせて最適化を行うので、それと合わせて、のちほど軽く触れます。
Frequency Conscious Signatures
「シグネチャの構築 (2) - 単語シグネチャの計算」では、単語シグネチャ計算時のハッシュ関数の数 k について解説しました。
また、「Bit-Sliced シグネチャ」では、転置した文書シグネチャにおいて、読み込む行数(の最大値)が k であることを説明しました。
k が小さいほど、読み込むビット数は必然的に小さくなります。
しかし、 k が小さすぎると誤検知が多発するようになってしまいます。
誤検知を一定以下に抑えつつ k をできるだけ小さくするにはどうすればよいでしょうか。
こちらも実は Higher Rank Rows 同様、制約つきの最適化問題として解くことができます。
そして Higher Rank Rows と同じように、単語ごとに最適な k も異なるため、単語ごとに(IDF ごとに)別々に最適化を施します。
Sharding by Document Length
BitFunnel アルゴリズムは検索処理を分割できるので、クラスタ構成での分散処理が可能です。

クラスタの各インスタンスにインデックス(シグネチャファイル)を分散して持たせることを考えたとき、ただ単に分割するよりも良い方法があります。
ここまで、文書シグネチャのサイズはすべて固定で考えてきました。 しかし、よく考えてみると、実際の Web の文書は、非常に短いものもあれば、数千の単語からなる長文も存在します。 文書長が違っていても同じビット数、同じハッシュ関数を使うのは効率がよくありません。
そこで、文書長が近いものを1つのシャードとしてまとめ、クラスタのインスタンスはシャードを単位としてインデックス(シグネチャファイル)を管理します。

赤く色づけされている列は、単語数の多い文書を表しています(ビット密度が高い)。 逆に、色がついていない列は、単語数の少ない文書を表しています(ビット密度が低い)。

ビット密度が高い文書(右)では長い文書シグネチャを、ビット密度が低い文書(左)では短い文書シグネチャを使うことで、より効率的になります。
BitFunnel アルゴリズムのパフォーマンス
以下は、論文の「6.2 Impact of Frequency Conscious Signatures and Higher Rank Rows」にあった実験結果の表です。

なお、 Treatment と書かれている列が、どの手法を使ったかを表しています。
それぞれ以下の通りです。
- BSS: 通常の Bit-Sliced シグネチャ
- BSS-FC: Bit-Sliced シグネチャ & Frequency Conscious Signature
- BTFNL: Bit-Sliced シグネチャ & Frequency Conscious Signatures & Higher Ranked Rows
また、 Density というのは、行のビット密度で、実験設定です。
BSS と BSS-FC 、Density が 0.15 の行に注目してみましょう。
通常の Bit-Sliced シグネチャに Frequency Conscious Signature を組み合わせると、ストレージ効率は3.2倍(46.7 -> 14.7 bits/postings)に、クエリ速度は2.6倍(9.1 -> 21.4 kQPS)になっています。
他の Density の行を見ても、この傾向は同じです。
つまり、Frequency Conscious Signatures はストレージ効率とクエリ速度をどちらも向上させることがわかります。
BSS-FC に、さらに Higher Ranked Rows を組み合わせた BTFNL を見てみます。
同じく Density が 0.15 の行を見てください。
すると、クエリ速度はさらに2.4倍(24.0 -> 57.0 kQPS)になっています。
一方、ストレージ効率は少ししか向上していません(bits/posting は少し下がっただけ)。
Higher Ranked Rows はクエリ速度に対する効果が大きいものの、ストレージ効率にはさほど効かないようです。
BitFunnel アルゴリズムを全文検索に使うときの注意点
シグネチャファイル方式の BitFunnel は、転置インデックス方式の検索エンジンとは性質が大きく異なるため、実際に適用するときには注意が必要でしょう。
具体的には、以下の点が気になります。 これらの問題を解決できれば Web 検索以外にも応用できそうです。
- false positive の扱い
- シグネチャファイルを使う以上、 false positive は必ず発生する
- 別のスコアリングシステムと併用することで false positive が下位になる
- (Web 検索ではヒット数が十分に多いので問題にならないことが多い)
- スコアリングの効率
- Bing では別のランキングシステム(機械学習によるスコアリングを行う)と併用
- ヒットした文書リストをすべて渡す必要がある
- ヒット数が非常に大きいときに、この処理をどうやって高速化しているのかはわからない
- FPGA を使った特殊なサーバを使っている?*15
まとめ
- 前半では、代表的な全文検索方式である転置インデックスとシグネチャファイルについて簡単に解説しました。
- 後半では、BitFunnel アルゴリズムを紹介しました。BitFunnel アルゴリズムがどのように検索速度やインデックスサイズを改善したかお分かりいただけたかと思います。
- BitFunnel アルゴリズムは、Web 検索以外にも応用できそうなので、用途を模索していきたいと思います。
参考文献
- BitFunnel: Revisiting Signatures for Search
- 元論文です。全文 PDF が無料でダウンロードできます。
- 情報検索アルゴリズム
- シグネチャファイルについて、「6.1 特徴ベクトルを用いた全文検索」を参照しました。
さらに学ぶために
- Introduction to Information Retrieval
- 情報検索の入門書のデファクトスタンダード。英語版なら無料で読めます。
- Information Retrieval: Implementing and Evaluating Search Engines
- 実装レベルで書かれている貴重な情報検索の教科書。
- 検索エンジン自作入門 ~手を動かしながら見渡す検索の舞台裏
- 転置インデックスを使った検索エンジンの実装について詳しく書かれています。
- 乱択アルゴリズム紹介(Bloom Filter) | Preferred Research
- ブルームフィルタの誤検出 (false positive) の確率について、コンパクトにまとまっています。
- Unix Magazine「インターフェイスの街角」 1999年11月号 「シグネチャ法によるお手軽検索システム」(PDF)
- Bit-String シグネチャを使った、シンプルな全文検索システムを C で実装しています。
*1:ACM (Association for Computing Machinery) の情報検索分科会。情報検索 (IR) 分野でのトップ会議です。URL は http://sigir.org/
*2:SIGIR 2017 の Best Paper にも選ばれています
*3:この記事でのアルゴリズムの解説は、論文をもとに書かれていますが、実際に Bing に実装されているものとは異なっている可能性があります
*4:転置インデックスにおいてキーとなるもの。単語ベースの方法では単語、文字ベースの方法ではテキストの部分文字列がトークンになります。
*5:興味のある方は、TAAT (Term At A Time), DAAT (Document At A Time), Top-k query などのキーワードで調べてみてください。たとえば転置インデックスとTop k-queryのスライドはおすすめです
*6:文字列の前処理や、ステミング(語幹の切り出し)や原形復元などの処理を行っている場合には発生することがあります。転置インデックス方式で false positive が発生するのは、転置インデックスという検索方式そのものにではなく、その他の部分に問題があります。
*7:文字ベースのインデックス(N-gram インデックス)を併用することで緩和できます。
*8:例では単語としていますが、N-gram の場合、出現位置の情報はほぼ必須です。
*9:転置インデックスについて、今回はただのマップとして扱いましたが、実用的な検索エンジンでは、インデックスは二次記憶上のファイルにシリアライズして書き出します。当然、動的な削除や更新は非常に難しくなります。詳しく知りたい方は、参考文献に挙げた情報検索の教科書や Apache Lucene の実装をあたるとよいでしょう。
*10:実際の検索エンジンでは、スコアリングや優先度つきキューを使ったソートなどを行って上位k件(Top-k)の検索結果を計算します
*11:ブルームフィルタのイメージをつかむには kumagi さんのスライドがよいでしょう。
*12:固定長のビットの並び。C++ では std::bitset Java では java.util.BitSet として実装されています
*13:実際にはもっと長いビットベクトルを使います。解説動画によると、実際の Web 検索では、典型的には1500ビットくらいのビットベクトルを使うそうです
*14:ハッシュ関数として使える関数は無限にありますが、実用的にはパフォーマンスや衝突確率などの観点から MD5, SHA1, MurmurHash あたりから選ばれることが多いようです。
